In this resource linked to COP27 in Egypt, maths students apply pythagoras’ theorem to solving Egypt’s road building conundrum.
Introduction/Motivation
The 2022 United Nations climate change conference (27th session of the Conference of Parties – COP27) will be held in Sharm El-Sheikh in Egypt, starting on the 7th of November.
In the introduction video screened at the end of COP26 in Glasgow, Egypt celebrates its road-building project. This resource explores efficient road designs and the climate impacts of car travel.
Resources:
Created with support from MEI
Section 1: Lesson Introduction
Show the Egypt introduction video from COP26 and show them the pictures of new Egyptian roads.
Road-building clip only:
Or the full Egypt introductory clip: from 09:21-12:26 in https://unfccc-cop26.streamworld.de/webcast/closing-plenary-of-the-cop-followed-by-cmp-and-c-2
Ask students what comments or questions they have on the video: What do they wonder?
They could discuss in pairs or groups before giving feedback to the class.
You could steer the discussion towards some of the following points:
- What are the advantages and disadvantages of building new roads?
- What do you thing about building new roads compared to the other climate mitigation and adaptation projects mentioned in the video?
- Roads for sustainable development: connecting cities and industry
- Will a new road reduce traffic?
- Building roads versus building railways/airports
- How will building new roads impact greenhouse gas emissions?
- Should houses be demolished to make way for new roads? https://www.reuters.com/world/middle-east/egypts-road-building-drive-eases-jams-leaves-some-unhappy-2021-05-14/
- How should governments decide which new roads to build? How can we reduce travel time for the most people, reduce the length of the new road or reduce the greenhouse gas emissions from people travelling on the road?
The remainder of the lesson uses maths to explore the last point.
Section 2: Scenario motivation for the Steiner problem
This could be introduced as motivation for the Steiner problem, or as a real world application once the problem has been solved (after section 3).
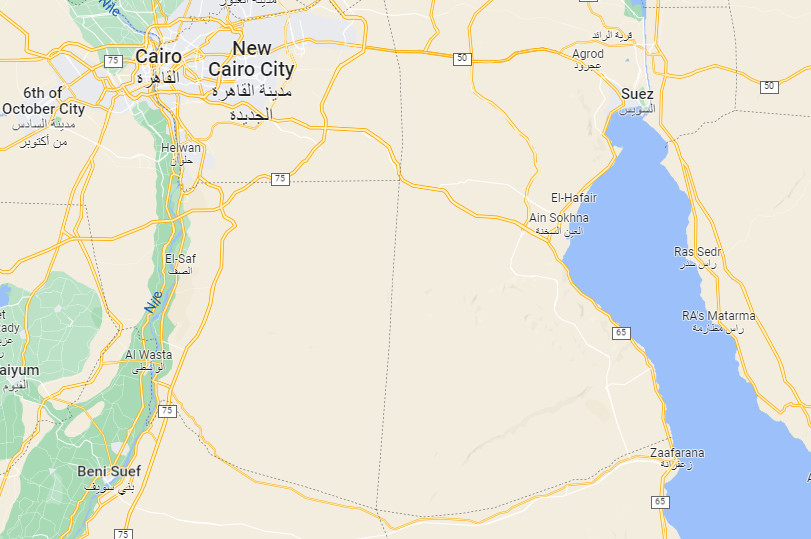
One of the new roads connects Beni Suef and Zaafarana. https://scoopempire.com/where-to-%EF%BB%BFegypt-launches-a-series-of-road-and-construction-projects-to-link-up-cities-far-and-wide/
Together with the important cities of Cairo and Suez, this can be simplified and framed as an example of the famous ‘Steiner Problem’:
Source: Google maps
Which looks a bit like:

Section 3: Steiner Problem using a Square
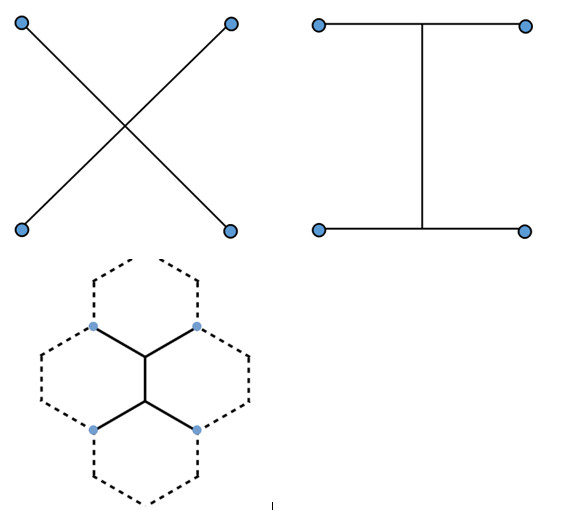
To simplify the problem, start by investigating 4 cities in a square. What is the most efficient way to connect all the cities (using the shortest distance of road)? You need to be able to visit all the cities on the road network, but you can go via other cities.
This problem is also described here: https://nrich.maths.org/14937
Students can use the sheet of squares (or squared paper) to draw as many different designs as they can think of, using curves and straight lines, or just straight lines.
Collect some ideas and ask students to calculate the total road distance required. For the square side length, you could use realistic road-distance numbers (eg 100km), simple numbers (eg 10, 1) or a symbol such as x. Students could first measure the distances using a ruler, then calculate them using Pythagoras’ theorem.
Help students to arrive at the optimal solution by considering the two designs below: Is there an intermediate design that would be even better?
Once students have arrived at the optimal solution, this video gives a good demonstration using soap bubbles: https://www.youtube.com/watch?v=dAyDi1aa40E
Section 4: Context Calculations
At this point you could choose to start using realistic road distances or the fact that the cities are not in a square but are closer to a rectangle (see the first extension point below).
- What is the total distance of the optimal network? How long would it take to travel between each city whilst travelling at the Egyptian motorway speed limit of 100km/hr? (https://www.autoeurope.ie/driving-information-egypt)
- Assume that the roads connecting Beni Suef to Cario, Cairo to Suez and Suez to Zaafarana already exist. Which one new road should be built to reduce the travel time from Beni Suef to Zaafarana? What is the reduction in travel time?
- Cars emit around 120 gCO2/km (https://www.eea.europa.eu/data-and-maps/indicators/average-co2-emissions-from-motor-vehicles/assessment-1)
By how much does the new road reduce the CO2 emissions of a journey from Beni Suef to Zaafarana? - Due to the shorter travel time, the new road might increases the number of journeys between Beni Suef and Zaafarana. How many extra journeys are needed to outweigh the decrease in emissions from the reduced distance?
Extension Ideas
- Return to the introduction video at the end of the lesson. What do students think about building roads and climate change after completing the activity?
• The 4 cities in Egypt are not in a perfect square, but are close to being in a rectangle. Does this change the optimal road network? This is discussed at https://thatsmaths.com/2015/01/29/the-steiner-minimal-tree/ - Students could use google maps to look at the real travel time between the 4 cities using different routes.
- What happens when we consider more cities?
- Can students think of other situations where this problem could apply? (gas pipelines, rail networks, broadband cables)
- Think about the real-world practicalities that the Steiner solution doesn’t address. Is it the best solution if most journeys are between Cairo and Suez? Should existing roads be removed in order to build the most efficient network? Which journey times would be increased by this?