Deep sea vents can emit harmful gases, such as hydrogen sulphide. Since these bubbles are small, they shrink once they leave the vent, as the gases dissolve into the ocean.
An autonomous submarine takes a photograph of these bubbles that looks like this graph sketch.
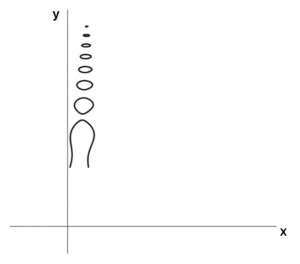
A scientist discovers that the surface of the bubbles visible in this photograph can be represented by the curve:
\[\sin\frac{y^{3}}{100} + e^{- x}y + x^{2} = 5\ ,\ y > 5\]
By first using implicit differentiation to show that
\[\frac{\text{dy}}{\text{dx}} = \frac{100(y – 2e^{x}x)}{3e^{x}y^{2}\cos\frac{y^{3}}{100} + 100}\]
Show that at the turning points on the curve, where \(\frac{\text{dy}}{\text{dx}} = 0\), \(y = 2xe^{x}\)
[8 marks]



